网络游戏同步

基本概念

网络游戏中，无论是多人pvp还是pve，都需要让所有玩家在除自己以外的玩家的客户端有表现，但由于网络延迟有可能会造成玩家游戏内容不同步，因此需要同步机制来确保所有玩家游戏内容的一致性。同步算法发展至今，大体可分为帧同步和状态同步两种方式。

帧同步

帧同步也被称作lockstep，锁步同步，原理十分简单：

相同的状态，接受相同的输入，执行相同的流程，到达新的相同状态。

可以从一个回合制游戏初步理解一下：

视频来自于宝可梦剑盾的联机对战，可以看到，游戏的每个回合双方玩家需要做出输入（选择宝可梦释放技能，使用道具或者交换上场…），在对战的双方确定输入后才会播放技能演示，进行逻辑处理（造成伤害，添加buff/debuff效果）并将游戏进程推进到下一个回合。

可以设想一下玩家可以控制宝可梦移动，不需要点选屏幕上的ui而是使用手柄按键来释放技能，做出输入的时间限制不是60秒而是60毫秒，游戏会变成什么样？显然，玩家移动摇杆后游戏内的角色能“立刻”走动，按下技能按钮也几乎能立刻看到技能效果，这也就是最原始的帧同步。

（顺带一提，暗黑破坏神2最开始也是设计成回合制游戏，后期通过减少回合的时长变成即时战斗）

如今的帧同步

经过多年的演化，现在的帧同步实现通常会设置一个转发服务器来接受所有客户端的指令，并下发数据包驱动客户端更新逻辑。

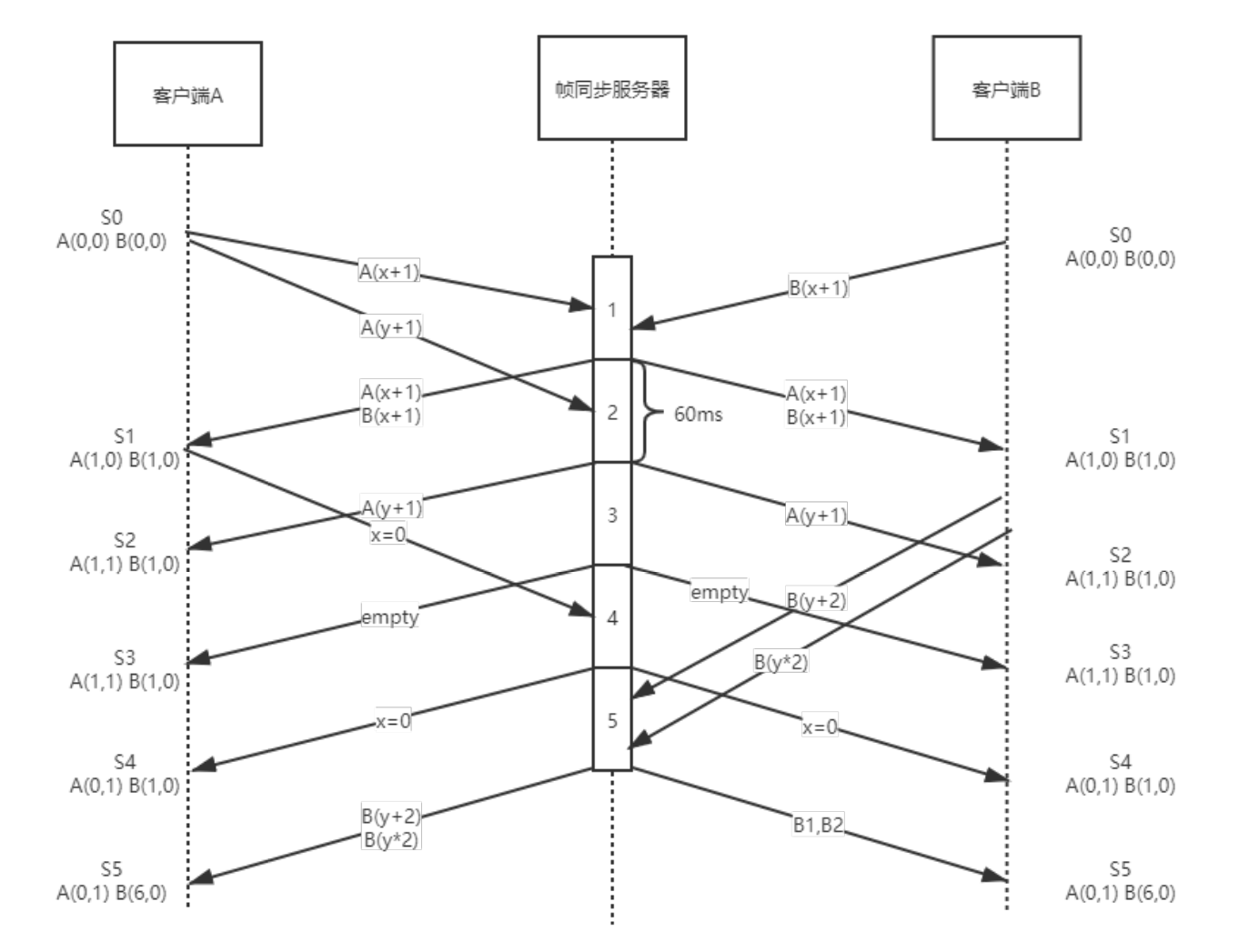
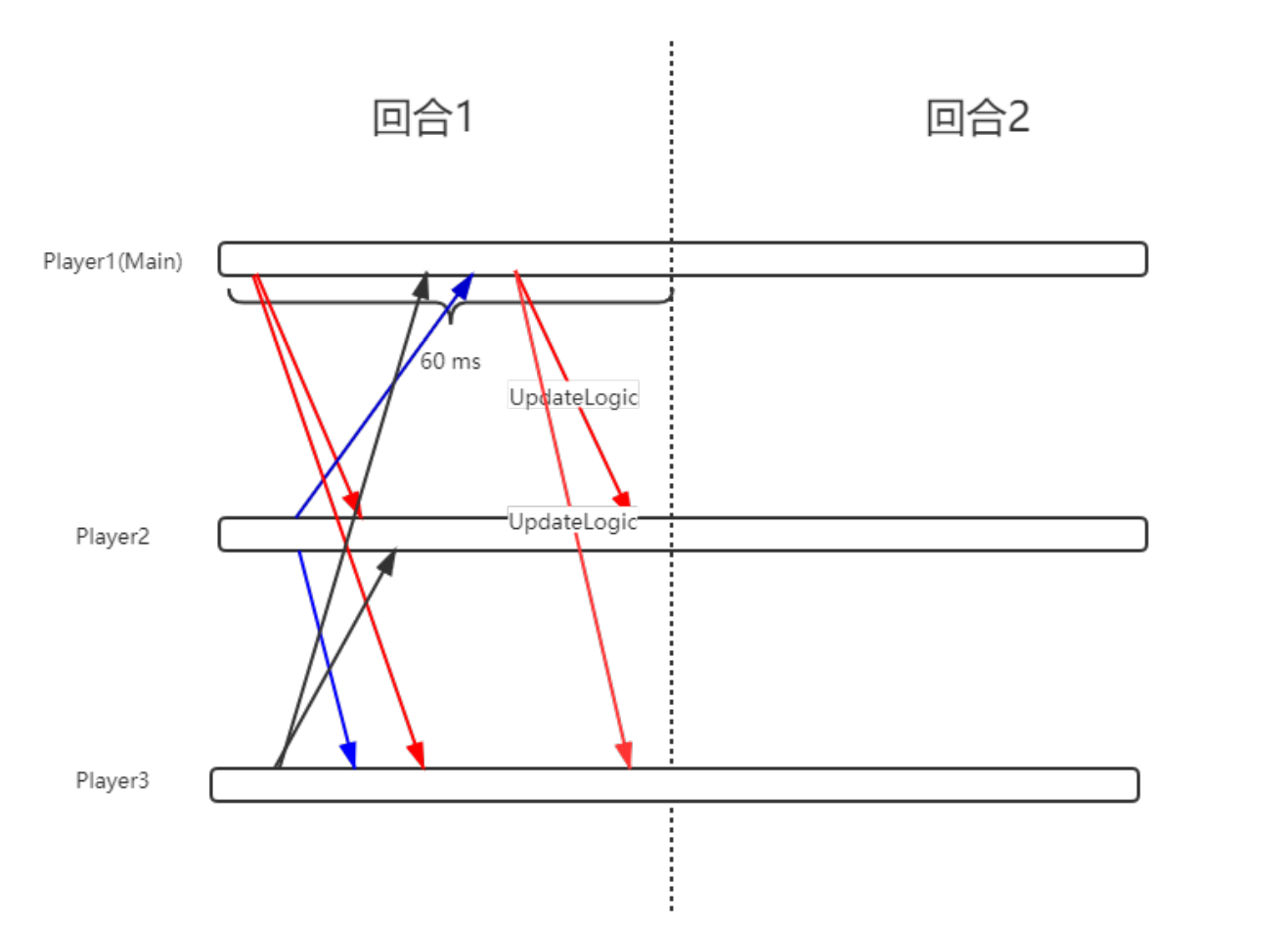
一个简单的例子，假设我们需要进行同步的是一个坐标，客户端A,B都有相同的初始状态A(0,0) B(0,0)。客户端A短时间连续操作，向服务器发出了A坐标x+1,y+1的指令，B客户端则向服务器发送了B坐标x+1的指令。在帧同步服务器的第一个逻辑帧内，A(x+1),B(x+1)的指令被服务器收到，服务器在帧末尾向A，B两个客户端转发这两条指令，客户端接受到服务器的驱动更新指令后进行逻辑更新，进入到一个新的状态S1 [A(1,0),B(1,0)] ，可以看到，虽然AB两个客户端进入到S1状态的时间不一样，但最终在逻辑更新后会达到同样的状态。

后续的逻辑帧更新类似，每一帧内服务器收到客户端的输入都会在帧末将这些指令转发到所有的客户端进行逻辑更新，如果游戏会在第N个逻辑帧结束，那么以这个算法来同步，可以保证AB两个客户端在所有的逻辑帧拥有相同的状态。

逻辑帧和渲染帧

这里需要注意区分逻辑帧和渲染帧，帧同步通常会将逻辑与渲染分离，逻辑更新指的是更新游戏内各种可交互实体的属性，比如角色位置，血量，技能CD，子弹位置…而渲染更新则是将显卡渲染好的一帧图像输出到显示器上进行展示。

为了让渲染帧的位置变化看起来顺畅自然，也需要使用一些预测算法，根据两个逻辑帧的状态插值过渡。人物运动行走有经典的航程算法(DeadRocking).

帧同步的优点

• 游戏逻辑没有服务器的概念，
• 网络传输只需要传输指令，相比状态同步十分节省网络流量。

帧同步的缺点

1.浮点数

相同的初始化状态和每帧相同的输入是容易保证的，但代码接受到同样的输入后有同样的状态变化却不是那么简单。

以根源的浮点数举例，不同平台的浮点数运算规则不一样，导致了物理引擎无法保证相同的物理逻辑更新在所有的客户端上有相同的结果，如果使用现成的物理引擎来实现帧同步游戏的物理计算，就很有可能违背代码接受到同样的输入后有同样的状态变化这一原则。

在windows和ubuntu平台下用同一份代码计算$x_{n+1}=f(x_n)=sin(x_n)$ 20次。

2.难以断线重连

帧同步的机制要求所有客户端都以初始状态从第一帧开始算，若玩家中途断线并且客户端没有了游戏当前的状态（杀进程），那么客户端需要从第一帧开始追帧，因为这个原因，帧同步也不太适合单局时长很长的游戏。

3.无法实现MMO类游戏

设想这样一个地图内可能有成百上千个玩家的MMORPG，在一帧内接受几百个输入并在客户端同时计算所有实体的游戏逻辑，无论是网络还是性能都是扛不住的。

4.没有办法反全图挂

虽然帧同步所有的逻辑都会运行在客户端，但一般的作弊帧同步也能够做得很好，可以看这篇文章

帧同步中的反外挂

大体的思路是服务器不仅承担收集转发指令的任务，还需要在游戏中或者结算的时候也运行游戏逻辑，来校验客户端的状态，不过因为单一的客户端拥有所有玩家的状态，面对全图挂是没有办法的。

快照同步

快照同步，只在服务器运行游戏逻辑，服务器运算得到结果后向所有的客户端广播。在这种同步算法下，客户端只是一个向服务器发请求并展示结果的纯表现终端，也有人认为这也算做状态同步的一种。

游戏体验时，玩家输入指令后明显感受到一段时间后才会有技能动画。对游戏响应性要求不高的游戏，比如棋牌，回合制通常会采用这种同步策略。

状态同步

帧同步通过同步操作，并根据操作进行相同的运算得到相同的结果，状态同步则直接同步状态。多数使用状态同步方案的游戏客户端和服务器都要运行游戏逻辑，不过客户端除了运行gameplay相关的逻辑还会有画面渲染，音效表现，服务器运行的是剔除了表现的纯逻辑。

客户端有丰富的表现：人物、枪械、场景，DS上只有各种碰撞框。

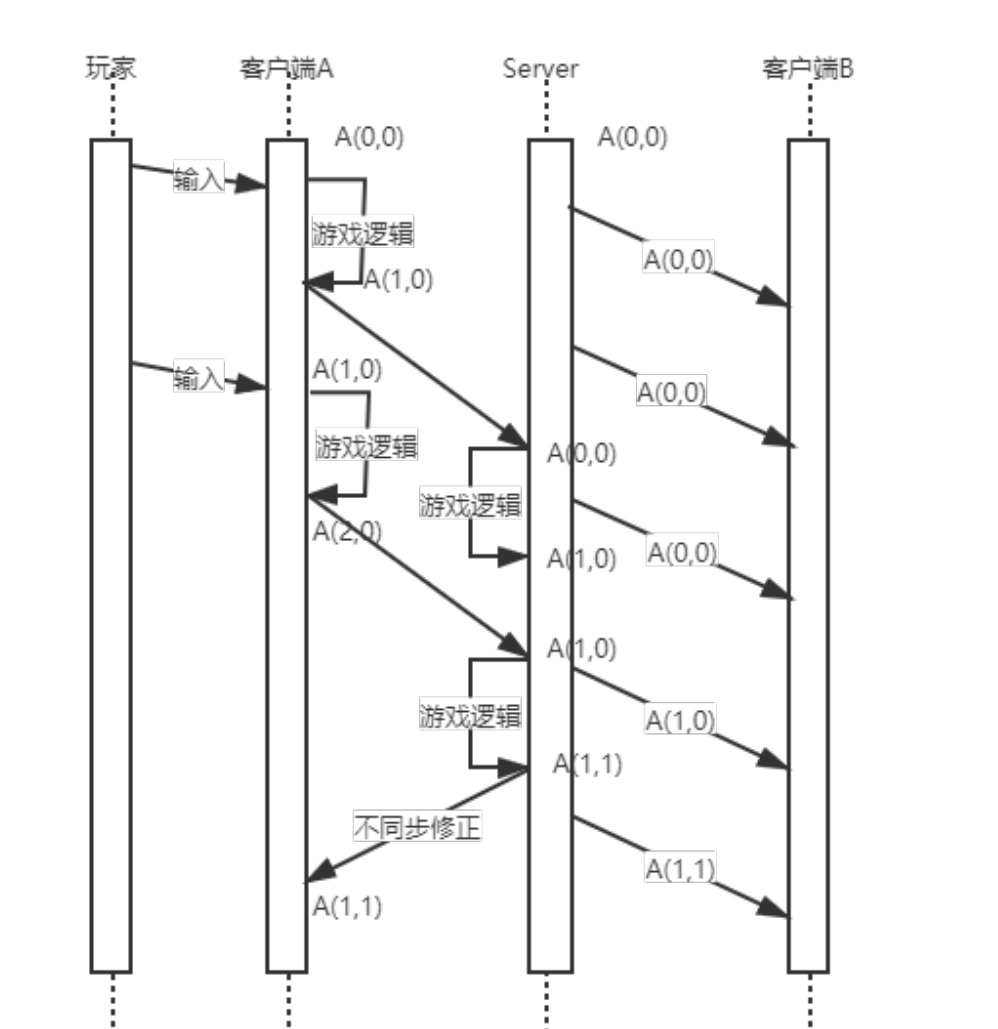
有预表现的状态同步的大致流程如下：

• 接受到玩家的输入后，客户端直接执行逻辑代码。
• 将运算的结果和玩家输入同时发送给服务器。
• 服务器收到客户端的输入后执行与客户端相同的逻辑代码。
• 服务器校验运算结果与客户端的运算结果，如果服务器与玩家客户端发送的运算结果一样，那么无事发生，如果不一样，服务器就会用服务器的运算结果修正客户端的状态。
• 将服务器的运算结果推送给第三方客户端。

状态同步的优点

• 相比帧同步需要等待服务器驱动，状态同步可以对输入做预表现，响应迅速。
• 天然支持断线重连，DS上拥有所有的信息，断线后只需要将这些信息发送给客户端。
• 性能优化容易，比如AI逻辑可以完全在DS上执行，客户端只需要表现位置变更动画表现以及放技能，一些复杂的逻辑也可以放在DS上做，客户端只做表现。

状态同步的缺点

• 流量较大，相比简单传输指令的帧同步，传输状态信息显然是需要更大的网络流量。
• 开发效率较低，每一个gameplay玩法都需要考虑客户端该怎么做，ds该怎么做，是否需要额外同步。
• 服务器开销较大，服务器通常要跑所有的游戏逻辑。

Participating Media Material

光的散射主要出现在参与介质的渲染中，关注点在于光子与组成参与介质的粒子进行交互的结果。光子在传播过程中遇到参与介质时，会有四种情况：

a.Absorption

光子被吸收转化为其他形式的能量，用$\sigma_a$来表示。

b.Out-scattering

光子被反射到当前光线传播路径之外的其他方向，类似不透明表面用BRDF来描述反射光线方向的分布，参与介质则用相函数(phase function)来描述反射光线方向的分布，用$\sigma_s$来表示。

c.Emission

当介质达到比较高的温度时，会发射出由热能转化来的光子。

d.In-scattering

既然Out-scattering会将当前传播路径的光子反射到其他方向，同理其他传播路径的光子也能反射到当前传播路径，并对最终的Radiance产生贡献，用$\sigma_s$来表示。

总而言之，Emission和In-scattering会对当前传播路径贡献光子，Absorption和Out-scattering则会消耗当前路径光子，这里需要引入一些定义：

消亡系数$\sigma_t=\sigma_s(Out-scattering)+\sigma_a$可以用来描述被消耗比率。

反照率定义为$\rho=\frac{\sigma_s}{\sigma_s+\sigma_a}=\frac{\sigma_s}{\sigma_t}$，反照率接近0时意味着光子几乎都是被介质吸收，像发电厂排放的黑烟就是这类介质，反照率为1意味着与介质接触的大部分光子都是被散射而不是被吸收，像云和大气就是这类介质。

在不考虑参与介质时，可以认为摄像机入射radiance等于与视线相交的最近表面的出射radiance，也就是$L_i(c,-v)=L_o(p,v)$，光线追踪便是基于这个原理从眼发射射线，最近相交表面的颜色也就是最终相机像素点的颜色。但如果考虑到参与介质，这个等式就不成立了，光线在参与介质中传播时与介质交互，radiance会发生变化，这个变化可以表述为：

$L_i(c,-v)=T_r(c,p)L_o(p,v)+\int_{0}^{||p-c||}T_r(c,c-vt)L_{scat}(c-vt,v)\sigma_sdt$

$T_r(a,b)=e^{-\sigma_td}$，$d$为a两点间的距离，这里是均匀介质才有$T_r(a,b)=e^{-\sigma_td}$，否则$T_r(a,b)=e^{-\int_a^b\sigma_t(x)d||x||}$，这个公式也被称作Beer-Lambert定理。

Inverse Transform Sampling

一个很重要的数学知识是逆变换采样，在算各种数值积分时会经常用到。众所周知计算机在生成随机数时只能生成均匀分布的随机数，但在进行重要性采样时需要得到密度函数$pdf(x)=f(x)$的采样分布，这里就需要用到逆变换采样。
具体的做法是

• 求累计密度函数$F_X(x)$，也就是$\int_{-\infty}^{x}f(x)dx$

• 计算$F_X(x)$的反函数$F_X^{-1}(x)$

• 生成区间$[0,1]$内的均匀分布采样点$U_i$

• 计算$X_i=F_X^{-1}(U_i)$，$X_i$也就是密度函数为$f(x)$的分布

ps:计算反函数$y=f(x)$，替换$xy$位置$x=f(y)$再次推导$y$的解析式就是反函数$f^{-1}(x)$了。

证明过程为：

设有分布$U$~$unif[0,1]$以及变换函数$T(U)=X$，经过变换后$X$满足累计密度函数$F_X(x)$，根据定义

$F_X(x)=P(X\leqslant x)=P(T(U)\leqslant x)=P(U\leqslant T^{-1}(x))$

而$U$是$[0,1]$内的均匀分布，$P(U\leqslant u)=u$，也就是$F_X(x)=P(U\leqslant T^{-1}(x))=T^{-1}(x)$

$F_X(x)=T^{-1}(x)$也就是$T(x)=F_X^{-1}(x)$

Importance Sampling

重要性采样需要生成与密度函数分布相同的采样点，也可以通过逆变换采样的方式将随机生成的均匀分布采样点投影到指定的密度函数。

以法线半球面均匀分布为例，其密度函数$pdf(h)=\frac{n·h}{\pi}$

用球面坐标可以表示为$pdf(\theta,\phi)=\frac{cos\theta sin\theta}{\pi}$

(这里可以理解为法线$n$是球坐标系的z轴，因此有$cos\theta=n·h$)

$pdf_{\Theta}(\theta)=\int_0^{2\pi}pdf(\theta,\phi)d\phi=2cos\theta sin\theta$

$cdf_{\Theta}(\theta)=sin^2\theta$

$pdf_{\Phi|\Theta}(\phi|\theta)=\frac{pdf(\theta,\phi)}{pdf(\phi)}=\frac{1}{2\pi}$

$cdf_{\Phi|\Theta}(\phi|\theta)=\frac{\phi}{2\pi}$

计算得到$cdf_{\Theta}(\theta)$以及$cdf_{\Phi|\Theta}$，就可以使用逆变换采样了，用Hammersley采样生成二维$[0,1]$均匀分布$X=(X_0,X_1)$

$cdf_{\Phi|\Theta}^{-1}(\phi)=2\pi \phi$

$\Phi_i=cdf_{\Phi|\Theta}^{-1}(X_0)=2\pi X_0$

$cdf_{\Phi|\Theta}^{-1}(\theta)=arcsin\sqrt{\theta}$

$\Theta_i=cdf_\Theta^{-1}(X_1)=arcsin\sqrt{X_1}$

最终得到的$(\Theta_i,\Phi_i)$就是法线半球面均匀分布的采样点，可以用这些采样点来计算表面的Irradiance…

PBR着色模型中的Specular BRDF类似，中间向量的分布密度函数$pdf(h)=D(h)(n·h)$，用球面坐标可以表示为$pdf(\theta,\phi)=D(h)cos\theta sin\theta=\frac{\alpha^2cos\theta sin\theta}{\pi(cos^2\theta(\alpha^2-1)+1)^2}$

$pdf_{\Theta}(\theta)=\int_0^{2\pi}pdf(\theta,\phi)d\phi=\frac{2\alpha^2cos\theta sin\theta}{(cos^2\theta(\alpha^2-1)+1)^2}$

$cdf_{\Theta}=\int_0^\theta pdf(\theta)d\theta=\frac{\alpha^2sin2\theta}{\pi((\alpha^2-1)cos^2\theta+1)^2}$

$pdf_{\Phi|\Theta}(\phi|\theta)=\frac{pdf(\theta,\phi)}{pdf(\phi)}=\frac{1}{2\pi}$

$cdf_{\Phi|\Theta}(\phi|\theta)=\frac{\phi}{2\pi}$

$\Phi_i=cdf_{\Phi|\Theta}^{-1}(X_0)=2\pi X_0$

$\Theta_i=cdf_\Theta^{-1}(X_1)=cos^{-1}\sqrt\frac{1-X_1}{(\alpha^4-1)X_1+1}$

镜面材质的全局光照实现方式大致也可以分为预计算和近似计算两种实现方式。

Localized Environment Maps

在Unity被称作Reflection Probe。

这种实现方式的原理与局部光照中的Specular IBL十分类似，主要有两点不同：

1.Specular IBL采样radiance的贴图是全局的EnvMap，LocalizedEnvMap则是在指定空间区域（多为立方体）内收集周围的radiance信息，在这个区域内的镜面材质物体着色才会使用这个LocalizedEnvMap。

2.Specular IBL中环境光被认为是从无穷远点入射到表面，因此直接使用视线反射向量来采样环境贴图并不会带来误差——相对于无穷远处，场景中的任意物体都可以视作在环境贴图的中心。但LocalizedEnvMap并不能这样处理，除非着色点正好位于作用区域的中心位置，越是偏离中心位置的着色点直接使用视线反射向量来采样LocalizedEnvMap产生的误差就会越大。

采样LocalizedEnvMap向量的计算方式如右图，首先根据视线向量$v$以及着色点法线$n$计算反射向量$r$，计算$r$与作用区域几何体的交点$p$，最终的采样向量$r`$为作用区域中心到交点$p$的向量。

除此之外，在Specular IBL中一些预处理的方法都可以用在LocalizedEnvMap，比如MipMap建立不同粗糙度的贴图，split-integral approximation等…

Planar Reflections

当要渲染的物体是一个平面时，可以通过直接渲染场景中其他物体与此平面的镜像来模拟镜面材质，这种方法十分简单易于理解，不仅能渲染完美镜面的反射效果，也能模拟带有一定粗糙度的光泽表面。缺陷在于消耗很大，相当于场景中的物体要被渲染两次。

Screen Space Methods

最常见的算法就是SSR以及基于这个算法的一系列改进和衍生算法。算法原理不难理解，大致的步骤为：

1.根据视线向量和着色点法线计算反射向量$r$

2.从着色点的空间位置（世界空间，视线空间，改进算法有投影到屏幕空间）开始，沿着反射向量$r$步进。

3.根据步进后迭代点投影到屏幕空间的坐标$P_{screenSpace}^i$在深度缓存中采样，判断缓存的深度是否比采样点的深度小，若是则认为光线与物体产生了交点，用$P_{screenSpace}^i$采样颜色缓存，作为入射方向$-r$的radiance贡献；反之则继续迭代步骤2，直到脱离场景。

原理虽然看起来比较简单，但如果就按这个思路去实现的话会发现效果几乎不能看，需要经过额外的优化算法才能有不错的效果，比如步进时不是每次增加固定长度而是二分查找，投影到屏幕空间进行迭代，对追踪起点做一些抖动…
有时间的话可以实现一下SSR算法。

全局光照除了处理遮挡关系的AmbientOcclusion之外，还有一个关键在于物体间的间接光照，回想局部光照模型中的光线路径会发现，无论是Diffuse还是Specular部分都可以用$L(D|S)E$来描述(L:光源 D:漫反射 S:镜面反射 E:眼)，也就是到达人眼时，光线仅经过了一次弹射。但实际上物体之间是会有间接光照的，真正的光线路径应该是$L(D|S)^*E$。实时渲染中并不能像光线追踪那般递归计算光线路径(消耗太大，光栅化架构也不合适)，因此在实时渲染中，全局光照多用预计算和高效近似计算两种方式来实现。

Surface Prelighting

简单来说就是将场景中的物体分为static和dynamic两类，static物体与光源以及其余static物体会在实时渲染之前使用离线渲染的算法预先计算好正确的光照交互的结果（通常是缓存Irradiance），实时渲染时只需要取出结果与表面材质进行计算。dynamic物体则还是使用LocalIllumination的模型进行光照计算，也可以使用一些近似算法来得到不那么PhysicallyBased的光照结果。

Unity的LightMap原理便是如此,可以参考shader中对LightMap的使用：

1
2
3

float4 albedo=tex2D(_MainTex,i.uv);
half3 lm = DecodeLightmap(UNITY_SAMPLE_TEX2D(unity_Lightmap, i.uv1));
float3 diffuse = albedo.rgb * lm;

不过预先计算表面Irradiance的方式是有缺陷的，在预计算时就需要得知法线的方向，无法在运行时通过法线贴图的方式得到更为精细的表面细节，因此又引申出了Directional Surface Prelighting

Directional Surface PreLighting

Directional Surface PreLighting的思路很简单，既然一个既定方向的Irradiance无法满足要求，那么可以把所有方向的Irradiance都预计算好，实时渲染时通过表面法线向量来索引取值。实际上这也是最常用的做法，预计算所有方向的Irradiance，通过数值积分的方式投影到球谐函数，在Texture中存储少量的球谐系数，实时渲染时通过球谐系数来重建光照信息，传入法线来获得Irradiance参与光照计算。通常而言投影到3阶球谐系数就能得到不错的结果，不过3阶系数需要9x3=27个float量，是简单Irradiance贴图的9倍消耗，因为这个原因也有一些优化的算法。

Volumeterically PreLighting

既然我们能将对静态物体的光照预计算结果存储于光照贴图并在实时渲染中使用，那么是否可以更进一步预计算存储场景中一些指定点（自动生成或人工指定）的Irradiance，实时渲染时用这些已知点的Irradiance信息通过插值的方式来查询场景中任意一点的Irradiance呢？答案是可以的，并且效果还不错，实际上多数游戏引擎对动态物体的GlobalDiffuseIllumination就是基于这个方法来实现的。

Irradiance Volume

这里有篇文章写很很好

IrradianceVolume是一个三维空间中的网格，类似下图：

图中规则排列的小球就是IrradianceVolume的节点。
构建IrradianceVolume常用的做法是在指定区域（自动或人工划分）用八叉树划分空间，为八叉树上的每个节点预计算当前空间位置的Irradiance信息（离线渲染，类似于烘焙LightMap），节点存储的并不是具体的Irradiance数值，而是Spherical Irradiance，即Irradiance随法线方向变化的函数，存储函数的方式则是将Spherical Irradiance投影球谐函数存储系数。

实时渲染使用IrradianceVolume则是查找着色点空间位置在八叉树中的划分，根据包围矩形8点顶点的预计算Irradiance信息，通过插值来获得着色点的Irradiance参与着色计算，插值方式根据划分的方式不同各有差异，比如三线性插值，立方体插值…

Unity Tetrahedral Interpolation

Unity引擎中实现dynamic物体的GlobalDiffuseIllumination组件是LightProbe，原理个人感觉与Irradiance Volume非常类似，只不过空间的划分和查找方式不一样。Unity采用四面体的方式来划分空间，实时渲染则查找包围四面体的四个节点来进行插值计算：

shader中的使用很简单，直接调用build-in函数ShadeSH9传入着色点法线就能获得着色点的Irradiance信息：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

// normal should be normalized, w=1.0
half3 SHEvalLinearL0L1 (half4 normal) ｛
    half3 x;
    // Linear (L1) + constant (L0) polynomial terms
    x.r = dot(unity_SHAr,normal);
    x.g = dot(unity_SHAg,normal);
    x.b = dot(unity_SHAb,normal);
    return x;
｝
// normal should be normalized, w=1.0
half3 SHEvalLinearL2 (half4 normal) ｛
    half3 x1, x2;
    // 4 of the quadratic (L2) polynomials
    half4 vB = normal.xyzz * normal.yzzx;
    x1.r = dot(unity_SHBr,vB);
    x1.g = dot(unity_SHBg,vB);
    x1.b = dot(unity_SHBb,vB);
    // Final (5th) quadratic (L2) polynomial
    half vC = normal.x * normal.x - normal.y * normal.y;
    x2 = unity_SHC.rgb * vC;
    return x1 + x2;
｝
half3 ShadeSH9 (half4 normal) ｛
    // Linear + constant polynomial terms
    half3 res = SHEvalLinearL0L1(normal);
    // Quadratic polynomials
    res += SHEvalLinearL2(normal);
    if (IsGammaSpace())
        res = LinearToGammaSpace(res);
    return res;
｝

环境光遮蔽的原理可以直接从渲染方程推导出来，对Lambertian表面，任意一个着色点p的渲染结果$L_o$是$\frac{c_{albedo}}{\pi}$和Irradiance的乘积，若假设在此着色点p的所有入射方向radiance为一常量$L_A$，也就是最简单的环境光Ambient Light，那么该点接受的Irradiance就为

$E(p,n)=\int_{l \in \Omega}L_A (n·l)^+dl=\pi L_A$

积分结果十分简单，不过有一些缺陷，这里并未考虑到着色点会被本模型的面片以及场景中其他模型面片的遮挡，若简单的假设面片被遮挡的方向入射radiance是0（实际上不是，有间接光照），未被遮挡的方向为$L_A$,设可见函数$v(p,l)$表明p点的l入射方向是否被遮挡，遮挡为0反之为1，那么Irradiance的积分就可以表示为：

$E(p,n)=L_A\int_{l \in \Omega}v(p,l)(n·l)^+dl$

定义遮蔽系数$k_A(p)$，代表点p未被遮蔽的入射方向百分比：

$k_A(p)=\frac{1}{\pi}\int_{l \in \Omega}v(p,l)(n·l)^+dl$

着色点的Irradiance就可以写成：

$E(p,n)=\pi K_AL_A$

除此之外，还可以使用BentNormal替代原来的法线取得更加精确的结果，BentNormal也就是未被遮蔽的平均方向。

$n_{bent}=(\int_{l \in \Omega}l v(p,l)(n·l)^+dl).normalize$

右图各点蓝色的方向就是该点的bent normal

Visibility And Obscurance

可见函数$v(l)$只有二值01在实时渲染的某些情况下是不太行得通的。设想在一个6个面都封闭的房间内，任选一个方向都最终会与墙壁或者房间内的物体相交，按照二值01定义，那么所有点的遮蔽系数$k_A(p)$都应为0。

(光线追踪可以递归跟踪得到被遮挡方向相交点的着色信息进而计算最终对当前着色点正确radiance的贡献，实时渲染无法得到)

在这种情况下，使用不那么物理正确的定义却能得到更好的效果，计算$k_A$时用distance mapping function $\rho(l)$来替代$v(l)$，$\rho (l)$的定义为：
$$\rho (l) = \begin{cases}
0 & {l与场景物体相交并且距离小于d_{max}} \
1 & {未与物体相交或相交距离大于d_{max}}
\end{cases}$$

$k_A$计算方式也就变成了：

$k_A(p)=\frac{1}{\pi}\int_{l \in \Omega}\rho(p,l)(n·l)^+dl$

使用$\rho (l)$代替$v(l)$的好处不仅在于不考虑自反射时渲染结果看起来更令人满意，还能起到加速计算的效果，超过$d_{max}$的物体可以不用参与遮蔽计算。

二值定义$v(l)$【左】与$\rho(l)$【右】的ao结果

Accounting for Interreflections

环境光遮蔽与真正的全局光照最大的区别大于Interreflections(自反射)，计算遮蔽时将被遮挡的入射方向的radiance贡献算作0，实际上并不会是0，在离线渲染的着色中就会递归的计算视线路径上的所有着色点的radiance贡献，限于计算消耗，这样的方法并不能用在实时渲染上。

不过好在有一些经验公式可以得到与全局光照接近的效果，替换遮蔽系数$k_A$为$k_A^·$

$k_A^·=\frac{k_A}{1-c_{albedo}(1-k_A)}$

可以理解为将ao系数适当的放大了一些，得到了类似考虑了自反射的效果。

Computation Of Ambient Occlusion

可以简单划分为两类，预先使用离线光追的方式计算ao贴图在实时渲染中使用，或者使用不那么PhysicallyBased的低消耗算法，如SSAO等。

Precomputed

其实就是算一个数值积分式，可以通过蒙特卡洛方法进行数值积分运算：

$k_A=\frac{1}{N}\sum_i^N v(l_i)(n·l_i)^+$

通过此式对要着色的物体的顶点生成ao值存放在贴图中，渲染时就可以直接从贴图中取值即可。

Dynamic Computation

比较基础且常见的就是SSAO了，以及其系列的衍生算法如HBAO…，这类算法的特点在于不那么物理正确，但在实时渲染中消耗较低，并且效果还算不错。后续该实现一下SSAO)

EnvMap不仅能用于光泽反射表面的着色，也可以对漫反射表面着色。相比用来渲染光泽表面的EnvMap存储radiance数值，通过视线反射向量来索引取值，用来渲染漫反射表面的EnvMap存储的是irradiance数值，通过着色点的法线来索引取值。

为什么要存储irradiance而不是像Specular IBL那样存储radiance呢？可以回顾一下理想漫反射表面的渲染方程：

$L_o=\int_\Omega f(l,v)L_i (n·l)dl=\frac{c_{albedo}}{\pi}\int L_i(n·l)dl=\frac{c_{albedo}}{\pi}E$

在渲染时我们只需要irradiance和表面的diffuseColor属性就能通过简单的乘法计算得到最终的着色结果。

预计算这个Irradiance EnvMap的过程就是一个数值积分，可以用重要性采样进行预估。

1

可以看到，包含高频信息的RadianceEnvironmentMap生成的IrradianceEnvironmentMap却只有低频信息，整个图像看起来十分模糊。这是必然的，Irradiance是法线半球上对radiance的积分，而环境贴图中相邻的法线间变化很小，两者积分半球区域几乎重叠，RadianceEnvironmentMap大部分radiance贡献都是共用（n·l有一些变化）。

缺少高频信息的IrradianceEnvironmentMap十分适合投影到球谐函数，在预处理时利用数值积分求解球谐系数存储，实时渲染中通过球谐系数来重建IrradianceEnvironmentMap用于渲染漫反射表面。相比CubeMap存储，投影IrradianceEnvironmentMap到球谐函数只需要存储少量系数就能达到差不多的效果，并且极大节省空间。实际上这也是大多数游戏引擎的做法。

Environment Map原本用于渲染镜面反射（roughness=0），经过一些改造，也能够用于渲染粗糙度不为0的光泽表面。
通过采集空间中给定点周围所有方向的radiance信息并存储到EnvMap中，对这个EnvMap进行一些处理就能模拟各种粗糙光泽表面。

Prfilter Environment Map

将原本用于渲染纯镜面的环境贴图进行模糊操作就能让使用这个环境贴图来渲染反射的表面看起来有’粗糙’的感觉：

模糊的方式有很多种(均值，高斯滤波…)，不过在进行模糊处理的时候并没有考虑表面的BRDF，更为合理的做法应该是根据表面的粗糙度，法线和视线方向生成一个Specular Lobe，并基于此对EnvMap进行模糊。

不过这样一来就会有多个参数共同控制Specular Lobe的形状，为每个参数存储一个预处理贴图是不现实的。因此在实际应用时需要对视线方向和法线方法做一些假设，这样预处理时就只需要给定不同粗糙度预计算生成环境贴图，并在实时渲染中根据粗糙度选取合适的贴图使用。这个结构和GPU的MipMap十分贴合，现在的实现也都是用不同级的MipMap存储粗糙度不同的贴图。

Split-Integral Approximation For Microfact BRDF

在微表面模型用环境贴图来渲染反射时，渲染方程有如下形式：

$f_{smf}(l,v)=\frac{F(h,l)G(l,v,h)D(h)}{4|n·l||n·v|}$

$L_{specularIBL}=\int_{l \in \Omega} f_{smf}(l,v)L_i(l)(n·l)dl$

数值积分求解在实时渲染中消耗太大，那么就需要近似方法：

$L_{specularIBL}=(\int_{l \in \Omega} D(r)L_i(l)(n·l)dl)(\int_{l \in \Omega}f_{smf}(l,v)(n·l))dl$

$r$是要采样的环境贴图的方向，这个方法也叫做split-integral approximation（这个近似看起来不那么物理，感觉上是看起来好就行的经验公式？）

经过分解后，第一个积分$\int_{l \in \Omega} D(r)L_i(l)(n·l)dl$只与表面粗糙度和反射向量相关，因为在预处理阶段无法确定法线方向n和视线方向v，只能假定$n=v=r$，在UE中的实现方式是：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

float3 PrefilterEnvMap( float Roughness, float3 R )
{
    float3 N = R;
    float3 V = R;
    float3 PrefilteredColor = 0;
    const uint NumSamples = 1024;
    for( uint i = 0; i < NumSamples; i++ )
    {
        float2 Xi = Hammersley( i, NumSamples );
        float3 H = ImportanceSampleGGX( Xi, Roughness, N );
        float3 L = 2 * dot( V, H ) * H - V;
        float NoL = saturate( dot( N, L ) );
        if( NoL > 0 )
        {
            PrefilteredColor += EnvMap.SampleLevel( EnvMapSampler , L, 0 ).rgb * NoL;
            TotalWeight += NoL;
        }
    }
    return PrefilteredColor / TotalWeight;
}

这个计算过程大致的思路是对法线方向用GGX分布进行重要性采样得到中间向量$H$，基于向量$H$计算视线向量$V$的反射向量$L$，所有采样点计算生成的$L$向量也就构成了在指定粗糙度(Roughness)和反射方向(R)的Specular Lobe，用$L$从EnvMap中采样取值平均，就得到了第一个积分式的数值积分结果。

第二个积分式$\int_{l \in \Omega}f_{smf}(l,v)(n·l)dl$ 在菲涅尔项使用Schlick近似时，$F_0$可以从积分中抽离出来：

$\int_{l \in \Omega}f_{smf}(l,v)(n·l)dl=F_0\int_{\Omega}\frac{f_{smf}(l,v)}{F(v,h)}(1-(1-v·h)^5)cos\theta_{l}dl+\int_{\Omega}\frac{f_{smf}(l,v)}{F(v,h)}(1-v·h)^5cos\theta_{l}dl=F_0*scale+bias$

抽离后可以发现在scale和bias的积分式中只有Roughness和$n·v$是变量：

$\frac{f_{smf}(l,v)}{F(v,h)}=\frac{D(h)G(l,v,h)}{4(n·l)(n·v)}$

UE中分别取不同的Roughness和$n·v$值预先计算这个数值积分并存放在一个2D LUT中，实时渲染时直接用Roughness和$n·v$索引取出scale和bias项，预计算的过程如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

float2 IntegrateBRDF( float Roughness, float NoV )
{
    float3 N=float3(0,0,1)
    float3 V;
    //BRDF各向同性，所以在NoV给定时，所有V值得到的结果是一样的，这里就是任取一个向量V
    V.x = sqrt( 1.0f - NoV * NoV ); // sin
    V.y = 0;
    V.z = NoV; // cos
    float A = 0;
    float B = 0;
    const uint NumSamples = 1024;
    for( uint i = 0; i < NumSamples; i++ )
    {
        float2 Xi = Hammersley( i, NumSamples );
        float3 H = ImportanceSampleGGX( Xi, Roughness, N );
        float3 L = 2 * dot( V, H ) * H - V;
        float NoL = saturate( L.z );
        float NoH = saturate( H.z );
        float VoH = saturate( dot( V, H ) );
        if( NoL > 0 )
        {
            float G = G_Smith( Roughness, NoV, NoL );
            float G_Vis = G * VoH / (NoH * NoV);
            float Fc = pow( 1 - VoH, 5 );
            A += (1 - Fc) * G_Vis;
            B += Fc * G_Vis;
        }
    }
    return float2( A, B ) / NumSamples;
}

综合两个分解积分式，实时渲染时IBL的着色就是：

1
2
3
4
5
6
7
8

float3 ApproximateSpecularIBL( float3 SpecularColor , float Roughness, float3 N, float3 V )
{
    float NoV = saturate( dot( N, V ) );
    float3 R = 2 * dot( V, N ) * N - V;
    float3 PrefilteredColor = PrefilterEnvMap( Roughness, R );
    float2 EnvBRDF = IntegrateBRDF( Roughness, NoV );
    return PrefilteredColor * ( SpecularColor * EnvBRDF.x + EnvBRDF.y );
}

环境光与面积光方向光类似，也是一种直接光照模型。

Ambient Light

Ambient Light是最简单的环境光模型，其radiance是一个常量数值，不会随着方向改变。当Ambient Light照射在漫反射表面时，得到的出射radiance $L_o$将会是一个常量值：

$L_o=\frac{\rho_{ss}}{\pi}L_A\int_{l \in \Omega}n·l dl=L_A*\rho_{ss}$

对任意BRDF的表面

$L_o=L_A\int_{l \in \Omega}f(l,v) n·l dl$

积分项$\int_{l \in \Omega}f(l,v) n·l dl$可定义为一个$R(l)$函数(directional-hemispherical reflectance)，实时渲染中常把此项简化为一个常数值$c_{amb}$，就有$L_o=c_{amb}L_A$，也就是代码中常见的:

1

L_ambient=Light_ambient*ambientColor

不过这里的着色是没有考虑物体间的相互遮挡的，因此一些凹陷处的颜色会比正确的结果要亮，为了解决这个问题也引申出了一系列计算遮蔽的方法。

Radiance Varying Light

区别于常量radiance的ambient light，另一种环境光形式则是radiance会随着方向变化。这种光源的radiance不是一个简单的数值，而是一个关于方向的函数。这个函数通常没有解析解(可以设想如何用一个函数表达式来描述大气层在照亮地面时的radiance)。因此，要在渲染中应用这种环境光，需要使用数值解，或是用函数近似的方式来实现。

Environment Mapping

将一个球面radiance函数记录在Texture上的方式也就是EnvironmentMapping了，是实时渲染中最常见的环境光表示方式。EnvironmentMapping优势在于简单高效，并且可以表示任意高频的radiance。因此，在需要渲染光泽材质时，就可以用EnvironmentMapping来记录周围环境的radiance信息，着色时只需要在着色点计算视线基于着色点法线的反射向量，在贴图中采样就能得到入射的radiance，也就是：

$r=2(n·v)n-v$

$L_i(v)=Sampler(EnvMapping,r)$

Specular Image-Based Lighting就是基于此实现的。

SphericalHarmonics

另外一种方式就是将环境光照投影到球谐函数，对于比较低频的光照信息，可以通过存储少量球谐系数来近似目标函数(参见SphericalHarmonics XD)。这个方法的优势在于相比EnvironmentMapping，所需要的存储空间极少。

精确光源(Punctual Light Source)

精确光源定义为立体角无限小的球面光源。在这无限小的立体角中，光线的radiance为$L_c$，定义其光源的颜色$c_{light}$为其垂直照射在反照率为$(1,1,1)$的Lambertian表面所得到的出射光radiance，即

$c_{light}=\lim_{\Omega \to 0} \frac{1}{\pi}\int_\Omega L_cd\omega$。

对任意表面，精确光源对出射角度为$v$的radiance的贡献为:

$L_o=\int_\Omega f_{brdf}(l,v)L_c(n ·l)^+d\omega$

实际上整个半球面只有精确光源所在的立体角内有入射光，因此

$\int_\Omega f_{brdf}(l,v)L_c(n ·l)^+d\omega=\lim_{\Omega \to 0}\int_\Omega f_{brdf}(l,v)L_c(n ·l)^+d\omega$

而极小立体角可视为l无变化

$L_o=f_{brdf}(n ·l)^+lim_{\Omega \to 0}\int_\Omega L_cd\omega=\pi f_{brdf}(n ·l)^+c_{light}$

面积光(Area Light Source)

面积光源则是在立体角$w_l$内有恒定的入射radiance $L_l$的光源，其对出射光方向$v$的radiance贡献则是在这个立体角范围内的积分：

$L_o=\int_{l \in w_l} f_{brdf}(l,v)L_l(n ·l)^+dl$

在实时渲染中对一个区域进行数值积分是不现实的，一个近似解决方案是用精确光源替代面积光

$L_o \approx \pi f_{brdf}(n ·l)^+c_{light}$

这个近似方案必然是有误差的，因为面积光源与着色点的立体角并不是精确光源那种理想化的极小值。不过这个误差可以人为把控，其主要受两个因素影响：一为源与物着色点的立体角，二为物体表面的粗糙度，因此，我们可以在仅用精确光源的情况下通过增加表面粗糙度来模拟面积光源照射的结果：

漫反射表面的面积光着色

对于理想Lambertian漫反射表面，用点光源来替换面积光源是不会引入误差的，其出射radiance可以通过iradiance得到：

$L_o(v)=\frac{\rho_{ss}}{\pi}E$

$\rho_{ss}$是表面材质属性中的反照率，irradiance $E$则可以通过积分计算：

$E=\int_{l\in w_l} L_l(n·l)^+dl \approx \pi c_{light}(n·l_c)^+$

即

$L_o(v)=c_{light}\rho_{ss} (n·l_c)^+$

也就是

1
2
3

lightDiff=lightColor*albedo*max(0,dot(n,l))

光泽表面的面积光着色

对光泽表面而言，最重要的视觉效果便是高光，我们在现实中可以观察到光泽表面的高光区域形状和大小与面积光源的形状大小类似，而其边缘会随着物体表面的粗糙度变化而有不同程度的模糊，这个现象引出了一些经验模型来近似面积光的照射结果。

一种近似方法是根据物体和光源的位置来修正材质的粗糙度属性:

$\alpha_g^·=(\alpha_g+\frac{r_l}{|p_l-p|})$

这个近似是十分高效的，只修改了粗糙度的数值，不需要加入额外的计算过程，在大多数时候可以得到比较好的视觉效果。不过当物体表面十分光滑类似于镜面时，这个近似的效果就不那么好了，粗糙度变大并不能模拟镜面反射面积光源的结果，反而会让镜面看起来有一些模糊。

另一种近似方法则是修正着色点到光源的向量，例如，球面光源可以选取距离视线反射向量最近的点代表整个光源，与着色点之间的向量作为光源向量参与计算：

设着色点为$p_{shade}$，那么修正后的光源向量$l_{light}=p_{cs}-p_{shade}$

取代表点的思路看起来像是蒙特卡洛方法中的重要性采样，当要计算区域中某个函数的积分值时，可以着重采样概率分布比较大的区域。更为严格的解释则是

[积分中值定理]：当函数$f(x)$在区间D内连续时,$\int_D f(x)dx=f(c)\int_D dx$

对于光照而言，函数f(x)为$f(x)=f_{brdf}(l,v)L_i(n·l)^+$,区域D则是着色点上半球面中面积光源与着色点形成的立体角。

从左到右依次为数值积分，修正粗糙度，修正光源向量的渲染结果。